


Thanks again.Ĭlick to expand.Hogan follow's Chaos Theory's smooth-course ("chunky"), smooth-course, smooth course, vertical continuity of planes, infinities of the two that reduce to the order of two, then overlaying and inlaying one into the other rise to the dimensionality of an infinite multi-dimensionality. I hope I provide the same help along the way to you and others, even if the energy initiated might be in opposition to some aspect or detail of the cosmological picture I'm advancing. I derive my picturing and modeling from the likes of Einstein and Hawking, but they are no help at all in helping me to surety and a fine detail and polish. You among some others, in expressing things the way you see them, do help me to greater clarification and confirmation of my own picture and modeling. How many different kind of measuring sticks, relatively speaking, would you have to use to measure point A to point B, and point B to point A, of what is in fact a naked singularity of distant Horizon (once more for emphasis, what is in fact exactly the same Horizon) in seemingly two different places, including, also seemingly, two different times? Talk about "quantum entanglement", that is entanglement to the extreme of entanglement where and when A is B and B is A : Where when a 0-dimensional point-singularity-balloon balloons big time to a relative extreme of large, and to a relative extreme of small. No difference whatsoever multi-dimensionally (Planck-Big Bang-Horizon). So exactly the same distance, dimensionally speaking, here to there there to here. The same Horizon (it overlays / inlays micro-macro / macro-verse | micro-verse - a nakedly singular Horizon far, far, outside us / and at once far, far, inside us). For higher-order derivatives, certain rules, like the general Leibniz product rule, can speed up calculations.Click to expand.You can't use a standard ruler to measure the distance from here to the Planck Horizon, therefore you can't use that ruler to measure the distance from here to the Big Bang Horizon. Additionally, D uses lesser-known rules to calculate the derivative of a wide array of special functions. It uses well-known rules such as the linearity of the derivative, product rule, power rule, chain rule and so on. Wolfram|Alpha calls Wolfram Languages's D function, which uses a table of identities much larger than one would find in a standard calculus textbook. For example, it is used to find local/global extrema, find inflection points, solve optimization problems and describe the motion of objects.

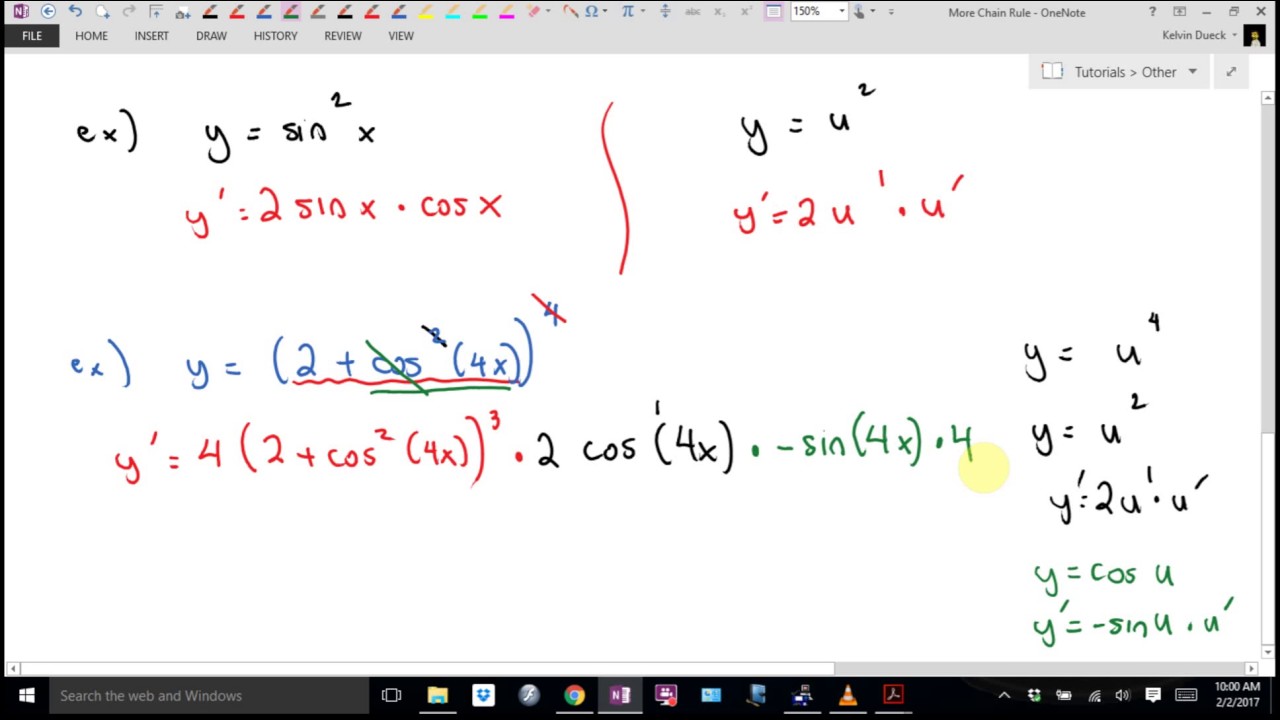
The derivative is a powerful tool with many applications. Īs an example, if, then and then we can compute. Geometrically speaking, is the slope of the tangent line of at. This limit is not guaranteed to exist, but if it does, is said to be differentiable at. Note for second-order derivatives, the notation is often used.Īt a point, the derivative is defined to be. These are called higher-order derivatives. When a derivative is taken times, the notation or is used. Given a function, there are many ways to denote the derivative of with respect to.
What are derivatives? The derivative is an important tool in calculus that represents an infinitesimal change in a function with respect to one of its variables.
#Infinitesimals to derive chain rule generator
Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator
#Infinitesimals to derive chain rule how to
Here are some examples illustrating how to ask for a derivative. To avoid ambiguous queries, make sure to use parentheses where necessary. Learn what derivatives are and how Wolfram|Alpha calculates them.Įnter your queries using plain English. Wolfram|Alpha is a great calculator for first, second and third derivatives derivatives at a point and partial derivatives. More than just an online derivative solver


 0 kommentar(er)
0 kommentar(er)
